Implementado una Red Neuronal Convolucional

Última actualización 09/05/2025

Open In Colab

#@title Importar librerías
#importar librerías necesarias
import random
from random import randint
import numpy as np
import pandas as pd
from tqdm.notebook import tqdm
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_openml
from sklearn.metrics import classification_report, confusion_matrix
import seaborn as sns
import random

import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras.layers import Dense, Dropout, Activation, Input
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.utils import to_categorical
from tensorflow.keras.datasets import mnist

#@title Funciones complementarias
def plot_samples_dataset(X, y):
    # Convertir las etiquetas a enteros
    y = y.astype(int)

    # Crear la grilla de 4x4
    fig, axes = plt.subplots(4, 4, figsize=(6, 6))
    fig.suptitle('Grilla de imágenes del dataset MNIST')

    # Iterar para mostrar las primeras 16 imágenes con sus etiquetas
    for i, ax in enumerate(axes.flat):
        img = X.iloc[i].values.reshape(28, 28)
        label = y[i]
        ax.imshow(img, cmap='gray')
        ax.set_title(f'Label: {label}')
        ax.axis('off')

    plt.show()

def plot_curva_aprendizaje(mlp):
    plt.figure(figsize=(8, 5))
    plt.plot(mlp.loss_curve_, marker='o')
    plt.title('Pérdida durante el entrenamiento del MLP por iteración')
    plt.xlabel('Iteración')
    plt.ylabel('Pérdida (Loss)')
    plt.grid()
    plt.show()

def plot_matriz_confusion(cm):
    # Visualizar la matriz de confusión usando Seaborn
    plt.figure(figsize=(10, 7))
    sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=range(10), yticklabels=range(10))
    plt.xlabel('Etiqueta predicha')
    plt.ylabel('Etiqueta real')
    plt.title('Matriz de Confusión para el MLP en el dataset MNIST')
    plt.show()

def encontrar_dim_imagen(n_neurons):
    """
    Encuentra la mejor forma cuadrada (filas, columnas) para una cantidad dada de neuronas.
    """
    side_length = int(np.sqrt(n_neurons))  # Calcular la raíz cuadrada del número de neuronas
    if side_length * side_length == n_neurons:
        return (side_length, side_length)  # Si es un cuadrado perfecto
    else:
        # Si no es un cuadrado perfecto, buscamos la mejor aproximación (filas, columnas)
        for i in range(side_length, 0, -1):
            if n_neurons % i == 0:
                return (i, n_neurons // i)  # Devolver filas y columnas
    return (n_neurons, 1)  # Si no encuentra, retornar en forma de vector (n_neurons, 1)

def plot_loss_historia_keras(history):
    # Graficar el histórico de pérdida durante el entrenamiento
    plt.plot(history.history['loss'], label='Pérdida de Entrenamiento')
    plt.plot(history.history['val_loss'], label='Pérdida de Validación')
    plt.title('Pérdida durante el Entrenamiento')
    plt.xlabel('Época')
    plt.ylabel('Pérdida')
    plt.legend()
    plt.show()

def plot_acc_historia_keras(history):
    # Graficar la precisión durante el entrenamiento
    plt.plot(history.history['accuracy'], label='Precisión de Entrenamiento')
    plt.plot(history.history['val_accuracy'], label='Precisión de Validación')
    plt.title('Precisión durante el Entrenamiento')
    plt.xlabel('Época')
    plt.ylabel('Precisión')
    plt.legend()
    plt.show()

def visualizacion_filtros_cnn_keras(model):
    # Obtener las capas convolucionales del modelo
    conv_layers = [layer for layer in model.layers if 'conv' in layer.name]

    # Definir la figura con una fila por capa convolucional y varias columnas (5 filtros al azar por capa)
    fig, axes = plt.subplots(len(conv_layers), 5, figsize=(10, len(conv_layers) * 3))

    # Recorrer cada capa convolucional y sus pesos
    for layer_index, (layer, ax_row) in enumerate(zip(conv_layers, axes)):
        # Obtener los pesos de la capa (solo el primer tensor, ignorar bias)
        layer_weights = layer.get_weights()[0]  # shape: (filter_height, filter_width, input_channels, num_filters)

        # Seleccionar 5 filtros de la capa actual
        num_filters = layer_weights.shape[-1]
        random_filters = random.sample(range(num_filters), 5)

        # Obtener los límites para la normalización de las imágenes
        vmin, vmax = layer_weights.min(), layer_weights.max()

        # Dibujar cada filtro seleccionado
        for filter_index, ax in zip(random_filters, ax_row):
            # Extraer el filtro correspondiente (shape: filter_height, filter_width, input_channels)
            filter_weights = layer_weights[..., filter_index]

            # Promediar los canales para visualizar como imagen en escala de grises
            if filter_weights.shape[-1] > 1:
                filter_weights = np.mean(filter_weights, axis=-1)  # Promedio sobre los canales de entrada

            # Dibujar la imagen del filtro
            ax.matshow(filter_weights, cmap=plt.cm.gray, vmin=0.5 * vmin, vmax=0.5 * vmax)
            ax.set_xticks([])
            ax.set_yticks([])
            ax.set_title(f'Capa {layer_index + 1}, Filtro {filter_index}')

    plt.suptitle('Visualización de Filtros de las Capas Convolucionales de Keras')
    plt.tight_layout()
    plt.show()

def visualizacion_feature_maps(model, image):
    # Crear un nuevo modelo que toma la misma entrada pero cuya salida son los mapas de características de cada capa convolucional
    layer_outputs = [layer.output for layer in model.layers if 'conv' in layer.name]
    feature_map_model = tf.keras.Model(inputs=model.input, outputs=layer_outputs)

    # Obtener los mapas de características al pasar la imagen a través del modelo
    feature_maps = feature_map_model.predict(np.expand_dims(image, axis=0))  # Añadir batch dimension

    # Recorrer cada capa convolucional y sus feature maps correspondientes
    for layer_index, feature_map in enumerate(feature_maps):
        # Número de filtros en la capa actual
        num_filters = feature_map.shape[-1]

        # Definir la figura con una fila por cada filtro (limitado a 6 para evitar gráficos muy grandes)
        fig, axes = plt.subplots(1, min(6, num_filters), figsize=(20, 5))

        # Mostrar cada filtro como imagen en escala de grises
        for i in range(min(6, num_filters)):  # Mostrar un máximo de 6 filtros
            ax = axes[i]
            # Extraer el feature map del filtro `i` y mostrarlo
            ax.matshow(feature_map[0, :, :, i], cmap='viridis')
            ax.set_xticks([])
            ax.set_yticks([])
            ax.set_title(f'Filtro {i+1}')

        # Título de la capa y ajuste de la visualización
        plt.suptitle(f'Visualización de Feature Maps - Capa {layer_index+1}')
        plt.tight_layout()
        plt.show()

Dataset MNIST (Clasificación multiclase)

Trabajaremos con el clásico dataset de imágenes de digitos escritos a mano. Esta dataset puede ser descargado de diversas fuentes incluido sklearn.

# Cargar el dataset de MNIST
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist['data'], mnist['target']

# Visualizamos algunas imágenes
plot_samples_dataset(X, y)

Un breve vistazo del dataset nos indica que la mayoría de pixeles de la imágen estan en 0 y que los que tiene valor estan en 255. Esta escala, es los valores de intensidad en escala de grises. Además, vemos que la información esta organizada en un dataframe con 784 columnas lo que se traduce en una versión vectorizada de una imágen de 28x28 píxeles.

X.describe()

	pixel1	pixel2	pixel3	pixel4	pixel5	pixel6	pixel7	pixel8	pixel9	pixel10	...	pixel775	pixel776	pixel777	pixel778	pixel779	pixel780	pixel781	pixel782	pixel783	pixel784
count	70000.0	70000.0	70000.0	70000.0	70000.0	70000.0	70000.0	70000.0	70000.0	70000.0	...	70000.000000	70000.000000	70000.000000	70000.000000	70000.000000	70000.000000	70000.0	70000.0	70000.0	70000.0
mean	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.197414	0.099543	0.046629	0.016614	0.012957	0.001714	0.0	0.0	0.0	0.0
std	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	5.991206	4.256304	2.783732	1.561822	1.553796	0.320889	0.0	0.0	0.0	0.0
min	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.0	0.0	0.0	0.0
25%	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.0	0.0	0.0	0.0
50%	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.0	0.0	0.0	0.0
75%	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000	0.0	0.0	0.0	0.0
max	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	...	254.000000	254.000000	253.000000	253.000000	254.000000	62.000000	0.0	0.0	0.0	0.0

8 rows × 784 columns

Antes de hacer la división del conjunto de datos, podemos hacer una normalización de los valores de los píxeles para que esten entre 0-1, así es más fácil para la red optimizar la función de pérdida.

# Normalización
X = X / 255.

# usar train test split para dividir los datos X y y
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    test_size=0.30,  random_state=42)

print('Dimensión X_train: {}'.format(X_train.shape))
print('Dimensión X_test: {}'.format(X_test.shape))

Dimensión X_train: (49000, 784)
Dimensión X_test: (21000, 784)

La entrada a una red CNN es diferente que las entradas para un MLP. En primera instancia debemos redimensionar nuestro vector de 784 pixeles en un arreglo de 28x28, lo cual representa nuestra imagen de digitos. Por otro lado, en las CNN es obligatorio agregar una tercera dimensión a la matriz de entrada, ya que las imágenes se representa por medio de canales. Cuando son en blanco y negro, se dice que solo tienen un canal y cuando son a color (RGB) son 3 canales.

n_muestras_train = X_train.shape[0]
n_muestras_test = X_test.shape[0]
dim_imagen = (28, 28)
n_canales = 1

# Aplicar el reespectivo redimensionamiento
X_train = np.reshape(X_train, (n_muestras_train,
                               dim_imagen[1], dim_imagen[1],
                               n_canales))
X_test = np.reshape(X_test, (n_muestras_test,
                               dim_imagen[1], dim_imagen[1],
                               n_canales))

print('Dimensión X_train: {}'.format(X_train.shape))
print('Dimensión X_test: {}'.format(X_test.shape))

Dimensión X_train: (49000, 28, 28, 1)
Dimensión X_test: (21000, 28, 28, 1)

Clasificador CNN multiclase en keras

Componentes base complementarios

Capas de Pooling
Capas de normalización

1. Capas de Pooling

2. Capas de normalización

En nuestro ejemplo, no es necesario normalizar ya que nuestras entradas estan entre 0 y 1 y no tienen un alta complejidad. Pero en otros escenarios, con imágenes más complejas y en formato RGB la normalización se hace más común.

# Asumiendo que X_train y y_train ya están definidos como en el ejemplo anterior
# Preprocesar las etiquetas para que sean categóricas (one-hot encoding)
y_train_categorical = to_categorical(y_train)
y_train_categorical

array([[1., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.],
       ...,
       [0., 1., 0., ..., 0., 0., 0.],
       [1., 0., 0., ..., 0., 0., 0.],
       [1., 0., 0., ..., 0., 0., 0.]])

# crear modelo usando el API funcional
def cnn_model(input_shape, num_classes):
    # Definir la entrada
    inputs = tf.keras.Input(shape=input_shape)

    # Primera capa convolucional y de pooling
    x = tf.keras.layers.Conv2D(32, kernel_size=(3, 3), activation="relu",
                               strides=(1, 1),
                               padding="valid")(inputs)
    x = tf.keras.layers.MaxPooling2D(pool_size=(2, 2))(x)

    # Segunda capa convolucional y de pooling
    x = tf.keras.layers.Conv2D(64, kernel_size=(3, 3), activation="relu",
                               strides=(1, 1),
                               padding="valid")(x)
    x = tf.keras.layers.MaxPooling2D(pool_size=(2, 2))(x)

    # Aplanar y añadir Dropout
    x = tf.keras.layers.Flatten()(x)
    x = tf.keras.layers.Dropout(0.5)(x)

    # Capa de salida
    outputs = tf.keras.layers.Dense(num_classes, activation="softmax")(x)

    # Crear el modelo usando la API funcional
    model = tf.keras.Model(inputs=inputs, outputs=outputs, name='cnn_keras')

    return model

# Ahora se definen los input shape y el numero de clases
input_shape = (dim_imagen[0], dim_imagen[1], n_canales)
num_classes = 10

# Crear el modelo cnn
cnn_keras = cnn_model(input_shape, num_classes)

# Visualizar el resumen del modelo
cnn_keras.summary()

Model: "cnn_keras"

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ input_layer (InputLayer)        │ (None, 28, 28, 1)      │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d (Conv2D)                 │ (None, 26, 26, 32)     │           320 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d (MaxPooling2D)    │ (None, 13, 13, 32)     │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ conv2d_1 (Conv2D)               │ (None, 11, 11, 64)     │        18,496 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling2d_1 (MaxPooling2D)  │ (None, 5, 5, 64)       │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ flatten (Flatten)               │ (None, 1600)           │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout (Dropout)               │ (None, 1600)           │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense (Dense)                   │ (None, 10)             │        16,010 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

 Total params: 34,826 (136.04 KB)

 Trainable params: 34,826 (136.04 KB)

 Non-trainable params: 0 (0.00 B)

# tambien es posible visualizar nuestra red en formato de grafo
tf.keras.utils.plot_model(cnn_keras, rankdir='LR',show_dtype=True)

# Compilar el modelo
cnn_keras.compile(loss='categorical_crossentropy',
            optimizer=SGD(),
            metrics=['accuracy'])

# Entrenar el modelo
history = cnn_keras.fit(X_train, y_train_categorical,
                    epochs=30,
                    batch_size=128,
                    validation_split=0.2,
                    verbose=1)

Epoch 1/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 32s 103ms/step - accuracy: 0.2604 - loss: 2.1329 - val_accuracy: 0.7763 - val_loss: 0.8651

Epoch 2/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 40s 100ms/step - accuracy: 0.7170 - loss: 0.8741 - val_accuracy: 0.8841 - val_loss: 0.4328

Epoch 3/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 41s 102ms/step - accuracy: 0.8282 - loss: 0.5398 - val_accuracy: 0.9079 - val_loss: 0.3207

Epoch 4/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 30s 98ms/step - accuracy: 0.8755 - loss: 0.4041 - val_accuracy: 0.9270 - val_loss: 0.2540

Epoch 5/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 42s 100ms/step - accuracy: 0.8992 - loss: 0.3252 - val_accuracy: 0.9372 - val_loss: 0.2167

Epoch 6/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 41s 101ms/step - accuracy: 0.9138 - loss: 0.2829 - val_accuracy: 0.9444 - val_loss: 0.1931

Epoch 7/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 41s 101ms/step - accuracy: 0.9231 - loss: 0.2526 - val_accuracy: 0.9512 - val_loss: 0.1733

Epoch 8/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 41s 99ms/step - accuracy: 0.9292 - loss: 0.2346 - val_accuracy: 0.9535 - val_loss: 0.1600

Epoch 9/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 30s 96ms/step - accuracy: 0.9350 - loss: 0.2114 - val_accuracy: 0.9570 - val_loss: 0.1478

Epoch 10/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 31s 100ms/step - accuracy: 0.9376 - loss: 0.2025 - val_accuracy: 0.9600 - val_loss: 0.1391

Epoch 11/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 42s 102ms/step - accuracy: 0.9452 - loss: 0.1841 - val_accuracy: 0.9620 - val_loss: 0.1314

Epoch 12/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 40s 99ms/step - accuracy: 0.9466 - loss: 0.1766 - val_accuracy: 0.9627 - val_loss: 0.1269

Epoch 13/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 30s 99ms/step - accuracy: 0.9497 - loss: 0.1683 - val_accuracy: 0.9649 - val_loss: 0.1202

Epoch 14/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 43s 105ms/step - accuracy: 0.9497 - loss: 0.1671 - val_accuracy: 0.9664 - val_loss: 0.1161

Epoch 15/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 30s 96ms/step - accuracy: 0.9530 - loss: 0.1590 - val_accuracy: 0.9683 - val_loss: 0.1109

Epoch 16/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 42s 99ms/step - accuracy: 0.9527 - loss: 0.1602 - val_accuracy: 0.9686 - val_loss: 0.1073

Epoch 17/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 41s 99ms/step - accuracy: 0.9549 - loss: 0.1468 - val_accuracy: 0.9685 - val_loss: 0.1040

Epoch 18/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 42s 102ms/step - accuracy: 0.9561 - loss: 0.1420 - val_accuracy: 0.9698 - val_loss: 0.1018

Epoch 19/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 39s 96ms/step - accuracy: 0.9587 - loss: 0.1382 - val_accuracy: 0.9705 - val_loss: 0.0985

Epoch 20/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 32s 103ms/step - accuracy: 0.9579 - loss: 0.1386 - val_accuracy: 0.9718 - val_loss: 0.0948

Epoch 21/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 40s 99ms/step - accuracy: 0.9611 - loss: 0.1306 - val_accuracy: 0.9710 - val_loss: 0.0932

Epoch 22/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 42s 103ms/step - accuracy: 0.9593 - loss: 0.1307 - val_accuracy: 0.9719 - val_loss: 0.0905

Epoch 23/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 40s 99ms/step - accuracy: 0.9597 - loss: 0.1280 - val_accuracy: 0.9717 - val_loss: 0.0887

Epoch 24/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 30s 99ms/step - accuracy: 0.9629 - loss: 0.1202 - val_accuracy: 0.9738 - val_loss: 0.0870

Epoch 25/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 31s 100ms/step - accuracy: 0.9644 - loss: 0.1226 - val_accuracy: 0.9735 - val_loss: 0.0851

Epoch 26/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 42s 104ms/step - accuracy: 0.9641 - loss: 0.1221 - val_accuracy: 0.9745 - val_loss: 0.0839

Epoch 27/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 39s 99ms/step - accuracy: 0.9659 - loss: 0.1155 - val_accuracy: 0.9742 - val_loss: 0.0822

Epoch 28/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 41s 99ms/step - accuracy: 0.9650 - loss: 0.1146 - val_accuracy: 0.9745 - val_loss: 0.0809

Epoch 29/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 41s 99ms/step - accuracy: 0.9648 - loss: 0.1158 - val_accuracy: 0.9746 - val_loss: 0.0815

Epoch 30/30

307/307 ━━━━━━━━━━━━━━━━━━━━ 31s 100ms/step - accuracy: 0.9655 - loss: 0.1112 - val_accuracy: 0.9764 - val_loss: 0.0780

plot_loss_historia_keras(history)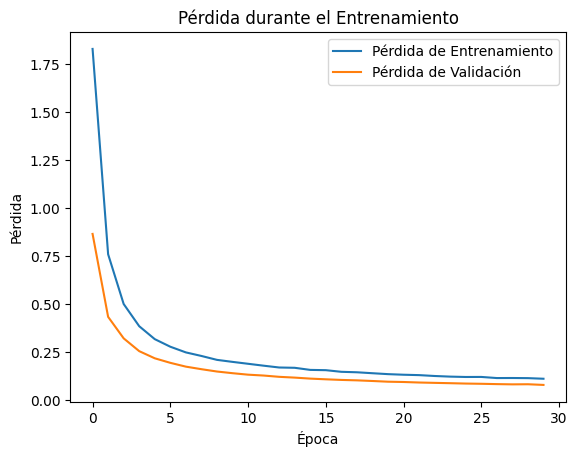

plot_acc_historia_keras(history)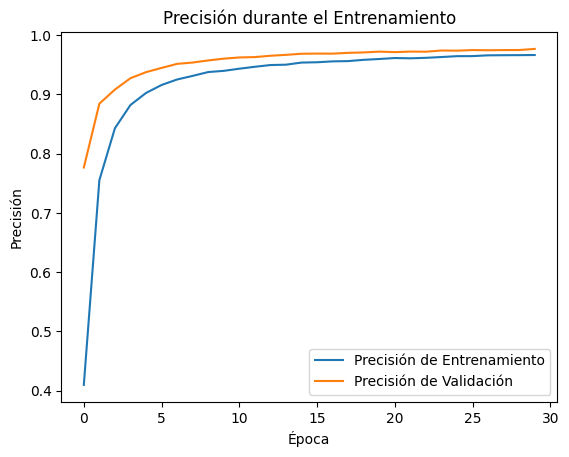

Evaluación completa

y_test_categorical = to_categorical(y_test)

score = cnn_keras.evaluate(X_test, y_test_categorical, batch_size=128)

score

165/165 ━━━━━━━━━━━━━━━━━━━━ 4s 24ms/step - accuracy: 0.9740 - loss: 0.0853

[0.08383515477180481, 0.9749523997306824]

# Realizar predicciones en el conjunto de prueba
y_pred = cnn_keras.predict(X_test)

# Convertir las predicciones en etiquetas (la clase con mayor probabilidad)
y_pred_classes = np.argmax(y_pred, axis=1)
y_true = y_test.values.astype(int)  # Las etiquetas reales del conjunto de prueba

657/657 ━━━━━━━━━━━━━━━━━━━━ 5s 8ms/step

# Generar el reporte de clasificación
print("Reporte de Clasificación para la red CNN en MNIST:\n")
print(classification_report(y_true, y_pred_classes))

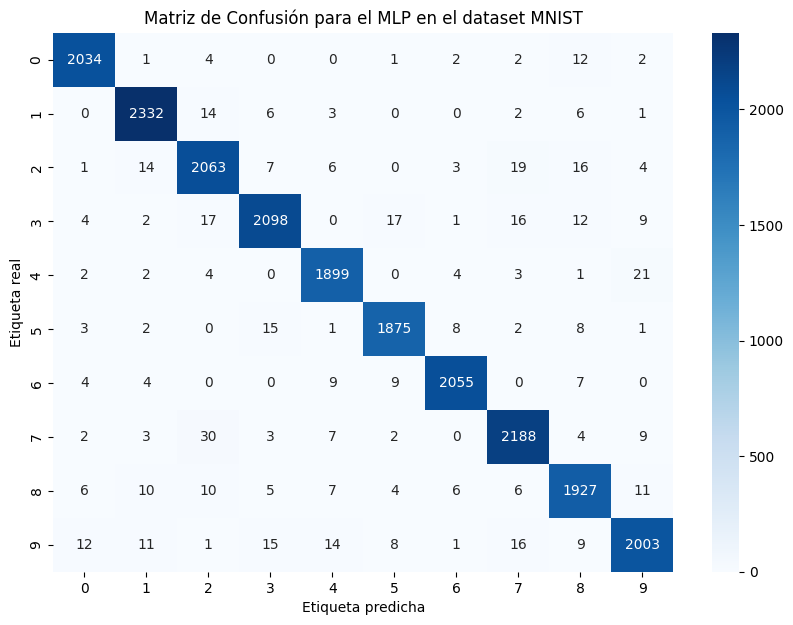
# Crear la matriz de confusión
cm = confusion_matrix(y_true, y_pred_classes)

# Visualizar la matriz de confusión usando Seaborn
plot_matriz_confusion(cm)

Reporte de Clasificación para la red CNN en MNIST:

              precision    recall  f1-score   support

           0       0.98      0.99      0.99      2058
           1       0.98      0.99      0.98      2364
           2       0.96      0.97      0.96      2133
           3       0.98      0.96      0.97      2176
           4       0.98      0.98      0.98      1936
           5       0.98      0.98      0.98      1915
           6       0.99      0.98      0.99      2088
           7       0.97      0.97      0.97      2248
           8       0.96      0.97      0.96      1992
           9       0.97      0.96      0.97      2090

    accuracy                           0.97     21000
   macro avg       0.97      0.97      0.97     21000
weighted avg       0.97      0.97      0.97     21000

Visualización de filtros convolucionales

visualizacion_filtros_cnn_keras(cnn_keras)

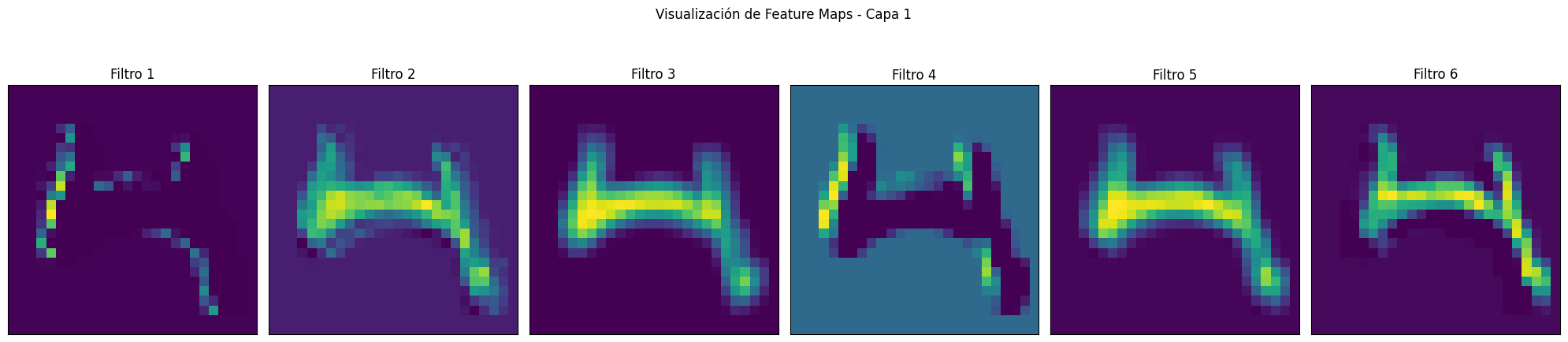
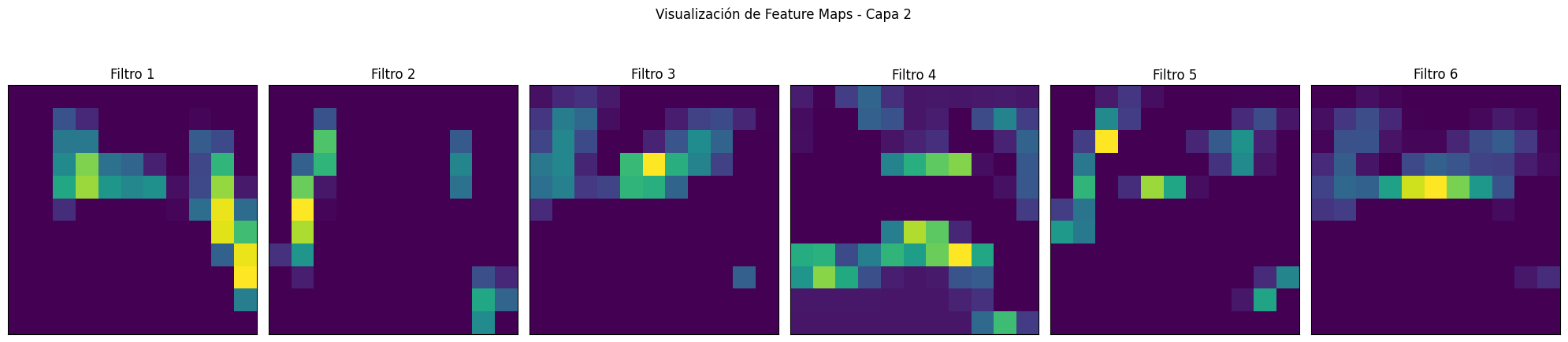
Visualización de los features maps

visualizacion_feature_maps(cnn_keras, image=X_test[randint(0, 100),:,:,:])

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 70ms/step